10418. Спасатели (бронза)
Фермер Джон открыл бассейн
для своих коров, полагая, что это поможет им расслабиться и произвести больше
молока.
В целях безопасности он
нанимает n коров в качестве спасателей, у каждой из которых
есть смена, охватывающая некоторый непрерывный промежуток времени в течение
дня. Для простоты пул открыт с момента t = 0 до времени t = 1000 ежедневно, поэтому каждую
смену можно описать двумя целыми числами, что дает время начала и окончания
смены коровы. Например, спасатель, начинающий в момент времени t = 4 и заканчивающийся в момент
времени t = 7, охватывает три единицы
времени (обратите внимание, что конечные точки – это “точки” во времени).
К сожалению, фермер Джон
нанял на 1 спасателя больше, чем у него есть средства для содержания.
Учитывая, что он должен уволить ровно одного спасателя, каково максимальное
количество времени, которое еще можно покрыть сменами остальных спасателей?
Промежуток времени покрывается, если присутствует хотя бы один спасатель.
Вход. Первая строка содержит количество спасателей n (1 ≤ n
≤ 100). Каждая из следующих n строк описывает спасателя в виде
двух целых чисел в диапазоне от 0 до 1000, задающих начальную и конечную точку
смены спасателя. Все такие конечные точки различны. Смены разных спасателей
могут совпадать.
Выход. Выведите одно число –
максимальное количество времени, которое еще можно покрыть, если фермер Джон
уволит 1 спасателя.
|
Пример
входа |
Пример
выхода |
|
3 5 9 1 4 3 7 |
7 |
РЕШЕНИЕ
перебор
Анализ алгоритма
Поскольку количество
спасателей и временные диапазоны
невелики, можно воспользоваться перебором. Посчитаем, сколько спасателей
покрывают каждый единичный отрезок времени. Перебираем каждого спасателя, удаляем
его из списка, вычисляем количество времени, которое покрывается
остальными спасателями. Среди всех таких времен ищем максимальное.
Временные
интервалы полуоткрытые. То есть если смена спасателя от a до b, то он
присутствует на работе в интервале [a; b) или в моменты времени от a до b – 1 включительно.
Пример
Занесем в cover[i] количество спасателей, которые покрывают интервал времени i.
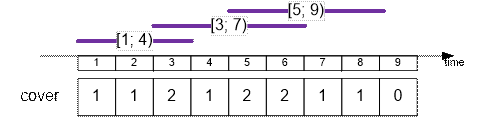
Удалим спасателя
со сменой [5;
9].
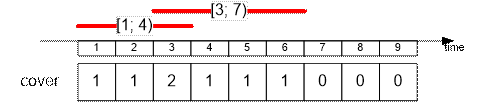
Оставшиеся спасатели покрывают 6 временных интервалов.
Удалим спасателя
со сменой [1; 4].
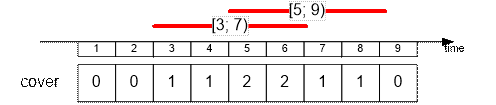
Оставшиеся спасатели покрывают 6 временных интервалов.
Удалим спасателя
со сменой [3; 7].
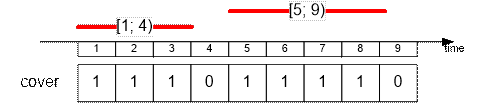
Оставшиеся спасатели покрывают 7 временных интервалов.
Оптимально
удалить спасателя со сменой [3; 7]. Остальные спасатели смогут покрыть наибольшее количество временных интервалов
– 7.
Реализация алгоритма
Объявим рабочие массивы.
vector<int>
start, fin, cover;
Читаем входные данные.
scanf("%d", &n);
start.resize(n
+ 1);
fin.resize(n
+ 1);
for(i = 0; i < n; i++)
scanf("%d %d", &start[i], &fin[i]);
В массиве cover подсчитаем,
сколько спасателей покрывают каждый интервал времени.
cover.resize(1001);
for (i = 0; i < n; i++)
{
for (j
= start[i]; j
< fin[i];
j++)
cover[j]++;
}
В переменной maxCover вычисляем
ответ.
maxCover
= 0;
Перебираем всех
спасателей.
for (i = 0; i < n; i++)
{
Уволим спасателя номер i.
for (j = start[i]; j < fin[i]; j++)
cover[j]--;
В переменной covered подсчитаем
количество интервалов, покрываемых оставшимися спасателями.
covered
= 0;
for (j = 0; j < 1000; j++)
if
(cover[j]
> 0) covered++;
Вычисляем максимум
среди всех возможных значений covered.
if (covered > maxCover) maxCover = covered;
Восстановим на работе спасателя
номер i.
for (j = start[i]; j < fin[i]; j++)
cover[j]++;
}
Выводим ответ.
printf("%d\n", maxCover);